Numerical Solutions on Tangled Mesh:
The Cauchy-Riemann equations for the velocity potential
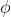 and the stream
function and the stream
function
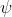 are solved by the discrete least-squares residual-minimization scheme:
the solutions and the nodal positions are computed by minimizing the residuals.
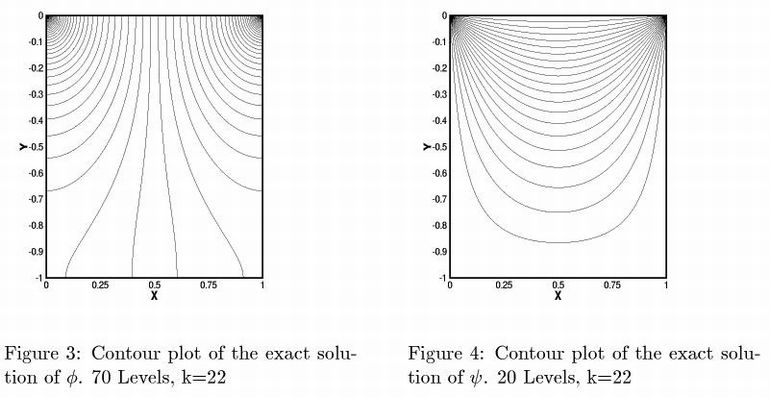
The exact solutions are available as shown in Figures 3 and 4 below.
are solved by the discrete least-squares residual-minimization scheme:
the solutions and the nodal positions are computed by minimizing the residuals.
The exact solutions are available as shown in Figures 3 and 4 below.
The initial regular triangular mesh (Figure 14) was adapted by the residual-minimization
and turned into as shown in Figure 15. It is
tangled due to aggressive mesh movement, with negative volumes
created. But the method converges simultaneously computing the solution on that
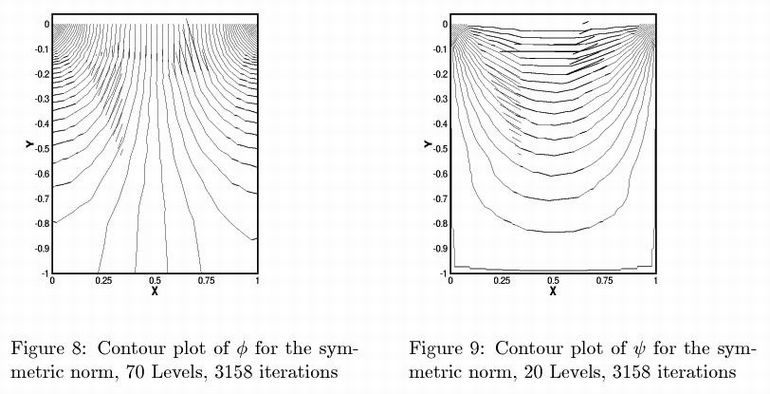
grid with no problems. The results are shown in Figures 8 and 9 below.
The solution contours look rather reasonable on such a bad mesh, don't they?
If you don't like the resulting grid, locally re-triangulate it (remove any
negative volume), and you'll have a reasonable solution on a valid grid.
It is nice that the computation never fails with negative volumes.
[Note: the solution and the grid points were solved simultaneously; the
grid converged first and then the solution converged later on that grid.]
See [ PhD Thesis ], Section 5.1, page 73, for the
residual-minimization scheme.
|

|

