CFD Notes by Hiroaki Nishikawa [Computational Fluid Dynamics

Diffusion Scheme for Discontinuous Data:

In finite-volume methods, the flux needs to be computed at the control-volume interface. For advection, the flux is computed given the left and right states extrapolated to the interface from the left and right cells. For diffusion, however, the focus is typically on the direct evaluation of the solution gradient at the interface. Here, we consider a diffusion scheme that is defined by the interface flux evaluated by the left and right states just like the advection scheme.

Consider the linear diffusion equation

$u_t = \nu u_{xx}$ ,

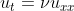which can be written as

$u_t + f_x = 0$ ,

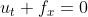where the flux is defined by

$f = - \nu u_x$ .

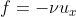We now consider solving this equation on a uniform mesh with cell-averaged solution values. oned_fv_data

Figure above shows reconstructed piecewise linear data commonly used to construct second-order advection schemes (MUSCL schemes of Van Leer). The left and right states at an interface, for example at face j+1/2, are given by

$u_L = u_j + \frac{1}{2} (u_x)_j \Delta x, \,\,\, u_R = u_{j+1} - \frac{1}{2} (u_x)_{j+1} \Delta x,$

where we assume that the gradients are evaluated by the central-difference formula,

$(u_x)_j=\frac{u_{j+1}- u_{j-1}}{2 \Delta x}, \,\,\, (u_x)_{j+1}=\frac{u_{j+2}- u_{j}}{2 \Delta x}, ........$ .

There is a useful diffusion scheme which can be directly applied to such data:

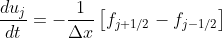$\frac{d u_j}{dt} = - \frac{1}{\Delta x} \left[ f_{j+1/2} - f_{j-1/2} \right]$ ,

where

$f_{j+1/2} = \frac{1}{2} ( f_L + f_R ) - \frac{\nu \alpha}{2 \Delta x} (u_R - u_L), \quad f_L = - \nu (u_x)_j, \quad f_R = - \nu (u_x)_{j+1}$ .

This is a second-order diffusion scheme. The first term in the numerical flux is called the consistent term (consistently approximates the diffusive flux) and the second term is called the damping term (provides damping for high-frequency errors). The damping term is very important, just like the dissipation is important for advection schemes, particularly on highly-skewed grids in multi-dimensions.

We find from truncation error (or Fourier) analysis the following special values of the damping coefficient, 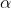$\alpha$ :

1. 2h-Laplacian Scheme (bad scheme): $\alpha = 0$

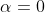
2. Central-Difference Scheme: $\alpha = 2$

3. 4th-Order Scheme (recommended): $\alpha = \frac{8}{3}$

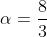
Note that the 2h-Laplacian scheme is a scheme with zero damping: the highest frequency cannot be damped (odd-even decoupling). The central-difference is nice since the stencil is compact (the 5-point stencil reduces to 3-point stencil automatically). The 4th-order scheme is nicer because it gives very accuarte solutions on irregular grids due to the strong damping (if not 4th-order accurate any more on irregular grids).

Anyway, the diffusion scheme that acts directly on the discontinuous data allows an easy extension of an advection code to an advection-diffusion code. Given the left and right states, we compute the advective and diffusive fluxes at once.

See [ AIAA2010-5093 ], Section 4.1.3, page 8, for more details on the above scheme (or CF2011).
See also [ Riemann solver for diffusion ] which proposes a similar diffusion scheme.

The alpha-scheme above has been found to be robust and accurate for unstructured grids [ CF2014 ], and has been used in practical CFD codes [ 2014 , AIAA 2020-3029 ] including a hypersonic-flow solver [ AIAA 2022-1848 ].

by Hiroaki Nishikawa, February 25, 2011 (updated February 13, 2022).

Back to Home